（本题满分12分）已知f(x)=x
-4x-4,x∈［t,t+1］(t∈R)，求f(x)的最小值φ（t）的解析式.
（本题满分12分）已知f(x)=x-4x-4,x∈［t,t+1］(t∈R)，求f(x)的最小值φ（t）的解析式.
解：f(x)=(x-2)
-8
(1)当2∈［t,t+1］时，即1＜t＜2时，φ(t)=f(2)=-8.（3分）
(2)t＞2时，f(x)在［t,t+1］上增函数，故φ(t)=f(t)=t-4t-4.（6分）
(3)当t+1＜2，即t＜1时，f(x)在［t, t+1］上是减函数.
故φ(t)=f(t+1)=t-2t-7（9分）
综上所述：φ(t)=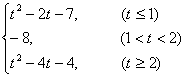
（等号位置可改变）（12分）