如图，已知圆M：x2+（y﹣4）2=4，Q是x轴上的动点，QA、QB分别切圆M于A，B两点．
（1）若点Q的坐标为（2，0），求切线QA、QB的方程；
（2）求四边形QAMB的面积的最小值及此时点Q的坐标；
（3）若AB=
，且Q在x轴正半轴上，求四边形QAMB外接圆的方程．
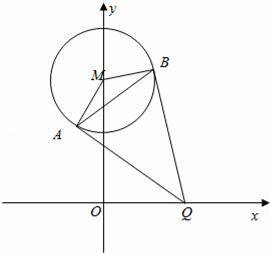
如图，已知圆M：x2+（y﹣4）2=4，Q是x轴上的动点，QA、QB分别切圆M于A，B两点．
（1）若点Q的坐标为（2，0），求切线QA、QB的方程；
（2）求四边形QAMB的面积的最小值及此时点Q的坐标；
（3）若AB=，且Q在x轴正半轴上，求四边形QAMB外接圆的方程．
【考点】直线与圆的位置关系；圆的切线方程．
【专题】综合题；直线与圆．
【分析】（1）设出切线方程，利用圆心到直线的距离等于半径，即可求切线QA、QB的方程；
（2）求出四边形QAMB的面积的表达式，利用|MQ|＞|MO|求出面积的最小值；
（3）设AB与MQ交于点P，通过MP⊥AB，MB⊥BQ，求出|MP|，求出|MQ|，确定Q的坐标，即可求四边形QAMB外接圆的方程．
【解答】解：（1）设过点Q的圆M的切线方程为x=my+2，﹣﹣﹣﹣﹣﹣
则圆心M到切线的距离为2，∴
=2，
∴m=﹣
或0，﹣﹣﹣﹣﹣﹣
∴切线QA、QB的方程分别为3x+4y﹣6=0和x=2﹣﹣﹣﹣﹣﹣
（2）∵MA⊥AQ，∴SMAQB=|MA|•|QA|=
≥
=
，此时Q（0，0）；﹣﹣﹣﹣﹣
（3）设AB与MQ交于点P，则MP⊥AB，MB⊥BQ，|MP|=
，
在Rt△MBQ中，|MB|2=|MP|•|MQ|，解得|MQ|=4
设Q（x，0），则x2+16=32，Q在x轴正半轴上，∴x=4
∴四边形QAMB外接圆的方程是（x﹣2）2+（y﹣2）2=8．﹣﹣﹣﹣
【点评】本题考查圆的切线方程的求法，四边形面积的求法，两点间的距离公式的应用，考查转化思想与计算能力．