,cos(α-β)=
,求tanα·tanβ的值. 
,cos(α-β)=,求tanα·tanβ的值. 解析:由已知得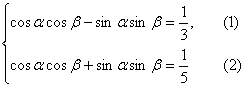
①+②得2cosαcosβ=,∴cosαcosβ=
.
②-①得2sinαsinβ=-
,∴sinαsinβ=-
.
∴tanα·tanβ=
·
=
=-
.
点评：要求cos(α+β)、cos(α-β)的值，需要知道sinα、cosα、sinβ、cosβ的值，也可以说知道cosαcosβ、sinαsinβ的值即可.反之，也可以由cos(α±β)的值，来确定cosαcosβ和sinαsinβ的值.这里采用对条件中复合角三角函数展开，再代数运算得结论，主要是观察到条件是复合角，结论是单角形式，函数名是正切的积的形式特征.