解：由方程组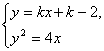
消去y,得k2x2+2(k2-2k-2)+(k-2)2=0.
（1）当k=0时，直线y=-2与抛物线y2=4x仅有一个公共点.
（2）当k≠0时，Δ=4(k2-2k-2)2-4k2(k-2)2=-16(k2-2k-1).
当k∈（1-
，0）∪（0，1+
）时，Δ＞0，直线与抛物线有两个公共点；
当k=1±
时，Δ=0，直线与抛物线仅有一个公共点；
当k∈（-∞，1-
）∪（1+
，+∞）时，Δ＜0，直线与抛物线没有公共点.
综合以上情况，当k∈（1-
，0）∪（0，1+
）时，直线与抛物线有两个公共点;当k=0或k=1±
时，直线与抛物线仅有一个公共点;当k∈（-∞，1-
）∪（1+
，+∞）时，直线与抛物线没有公共点.