=λ
.
(1)当λ=3时，求EF与平面ABCD所成的角：
（2）当λ=1时，求二面角F—DE—C的大小（用反三角函数表示）；
（3）当λ为何值时，有BD1⊥EF？
=λ.
(1)当λ=3时，求EF与平面ABCD所成的角：
（2）当λ=1时，求二面角F—DE—C的大小（用反三角函数表示）；
（3）当λ为何值时，有BD1⊥EF？
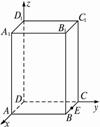
解：(1)如图建立空间直角坐标系，则D（0，0，0），E（1，2，0）.
当λ=3时，F（0，2，1），
=（-1，0，1）.
设平面ABCD的法向量为n,
则n=(0,0,1).
设与n的夹角为θ,
则cosθ=
=
.
∴EF与平面ABCD所成的角为45°.
(2)当λ=1时，F（0，2，2），
=（-1，0，2），
=（0，2，2）.
设平面DEF的法向量为m,则m
=0，m
=0，
∴m=(2,-1,1),
∴cos〈m,n〉=
=
.
∴二面角F—DE—C的大小arccos
.
(3)显然D1（0，0，4），B（2，2，0），设F（0，2，t）,
则=（-1，0，t），
=（-2，-2，4）.
要使EF⊥BD1，只要·=0，2+4t=0,t=-
.
∴λ=-9.