(1+x2)对一切实数x都成立? 
(1+x2)对一切实数x都成立? 解析:因为抛物线过点(-1,0),所以a-b+c=0.
又x≤f(x)≤ (1+x2)对一切实数x都成立,则由x=
(1+x2),得x=1.
故f(1)=a+c=
.
当x=0时,0≤f(0)≤
,即0≤c≤
,
所以0≤a≤
,且c=
-a.
此时“x≤f(x) 
(1+x2)对一切实数x都成立”可转化为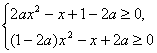
的解集为R.
当a=0或
时,上述不等式组不能恒成立;
当0＜a＜
时,
由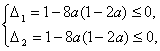
得(4a-1)2≤0,
所以a=
,c=
.
综上,当a=c=
,b=
时,原不等式对一切实数x都成立.