(本小题满分16分)
已知函数
（
，实数
，
为常数）．
（1）若
（
），且函数
在
上的最小值为0，求
的值；
（2）若对于任意的实数
，
，函数在区间
上总是减函数，对每个给定的n，求的最大值h(n)．
(本小题满分16分)
已知函数（，实数，为常数）．
（1）若（），且函数在上的最小值为0，求的值；
（2）若对于任意的实数，，函数在区间上总是减函数，对每个给定的n，求的最大值h(n)．
解：（1）当
时，
．
则
．
令
，得
（舍），
．…………………3分
①当
>1时，
|
| 1 |
|
|
|
|
| - | 0 | + | |
|
|
| ↘ |
| ↗ |
∴当时, 
．
令
，得
． ……………………………5分
②当
时，
≥0在
上恒成立，
在
上为增函数，当
时, 
．
令
，得
（舍）．
综上所述，所求
为
． ……………………………7分
(2) ∵对于任意的实数
，
，
在区间
上总是减函数，
则对于x∈(1,3)，
＜0，
∴
在区间[1,3]上恒成立． ……………………9分
设g(x)=
，
∵
，∴g(x)
在区间[1,3]上恒成立．
由g(x)二次项系数为正，得
即
亦即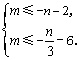
………12分
∵ 
=
，∴ 当n＜6时，m≤
，
当n≥6时，m≤
， ……………………………14分
∴ 当n＜6时，h(n)= 
，
当n≥6时，h(n)= ，
即
……………………………16分
