如图，矩形ABCD的边AB=6 cm，BC=8cm，在BC上取一点P，在CD边上取一点Q，使∠APQ成直角，设BP=x cm，CQ=y cm，试以x为自变量，写出y与x的函数关系式.并求
为何值时，
有最大值或最小值？
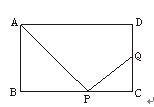
如图，矩形ABCD的边AB=6 cm，BC=8cm，在BC上取一点P，在CD边上取一点Q，使∠APQ成直角，设BP=x cm，CQ=y cm，试以x为自变量，写出y与x的函数关系式.并求为何值时，有最大值或最小值？
解：∵∠APQ=90°,
∴∠APB+∠QPC=90°。
∵∠APB+∠BAP=90°,
∴∠QPC=∠BAP，∠B=∠C=90°。
∴△ABP∽△PCQ。
∴
=－
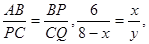
2+
．
当=4时，有最大值
解析:略