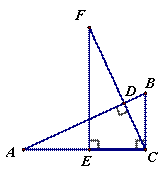
еҰӮеӣҫпјҢеңЁв–іABCдёӯпјҢвҲ ACB=90В°пјҢCDвҠҘABдәҺзӮ№DпјҢзӮ№EеңЁACдёҠпјҢCE=BCпјҢиҝҮзӮ№EдҪңACзҡ„еһӮзәҝпјҢдәӨCDзҡ„延й•ҝзәҝдәҺзӮ№F.
жұӮиҜҒпјҡAB=FC.
В

еҰӮеӣҫпјҢеңЁв–іABCдёӯпјҢвҲ ACB=90В°пјҢCDвҠҘABдәҺзӮ№DпјҢзӮ№EеңЁACдёҠпјҢCE=BCпјҢиҝҮзӮ№EдҪңACзҡ„еһӮзәҝпјҢдәӨCDзҡ„延й•ҝзәҝдәҺзӮ№F.
жұӮиҜҒпјҡAB=FC.
В

иҜҒжҳҺпјҡвҲөEFвҠҘAC
вҲҙвҲ FEC = 90В°= вҲ ACB
 вҲҙвҲ F +вҲ FCE = 90°    В
вҲҙвҲ F +вҲ FCE = 90°    В
вҲөCDвҠҘAB
вҲҙвҲ ADC = 90В°
вҲҙвҲ A +вҲ FCE = 90°        В
вҲҙвҲ F = вҲ AВ В В В В В В В В В В В
еңЁв–іFECе’Ңв–іACBдёӯВ
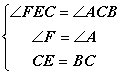
вҲҙ в–іFEC вүҢ в–іACB (AAS)В В В
вҲҙ FC = ABВ В В В В В В В В В В