已知函数![]()
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若存在![]() ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
已知函数![]()
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若存在![]() ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
(1)![]()
![]() 时
时![]()
![]()
![]()
![]()
![]() 在
在![]() 处的切线方程为
处的切线方程为![]() …3分
…3分
(2)![]()
![]() ,
,
所以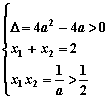 ,所以
,所以![]() . …6分
. …6分
(3)由![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() .
.
而![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 在
在![]() 上单调递增. …7分
上单调递增. …7分
∴在![]() 上,
上,![]() . …8分
. …8分
所以,“存在![]() ,使不等式
,使不等式![]() 恒成立”等价于“不等式
恒成立”等价于“不等式![]() 恒成立”,
恒成立”,
即,不等式![]() 对任意的
对任意的![]() (
(![]() )恒成立. …9分
)恒成立. …9分
令![]() ,则
,则![]() .
.
![]() . …10分
. …10分
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上递减.
上递减.
![]() ,不合题意.
,不合题意.
②当![]() 时,
时,![]() .
.
若![]() ,记
,记![]() ,则
,则![]() 在
在![]() 上递减.
上递减.
在此区间上有![]() ,不合题意.
,不合题意.
因此有 ,解得
,解得![]() ,
,
所以,实数![]() 的取值范围为
的取值范围为![]() . …14分
. …14分