已知函数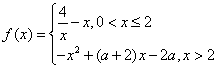
，其中
为实数．
（1）若函数
为定义域上的单调函数，求的取值范围．
（2）若
，满足不等式
成立的正整数解有且仅有一个，求的取值范围．
已知函数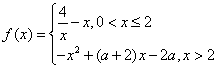，其中为实数．
（1）若函数为定义域上的单调函数，求的取值范围．
（2）若，满足不等式成立的正整数解有且仅有一个，求的取值范围．
解：（1）由题意，当
时，
为减函数，
当
时，
，
若
时，也为减函数，且
，
此时函数为定义域上的减函数，满足条件；
若
时，在
上单调递增，则不满足条件．
综上所述，．…………………………………..4分
（2）由函数的解析式，可得
，
当
时，
，不满足条件；
当
时，为定义域上的减函数，仅有
成立，满足条件；
当
时，在上，仅有，
对于上，的最大值为
，
不存在
满足，满足条件；
当
时，在上，不存在整数满足，
对于上，
，
不存在满足，不满足条件；综上所述，