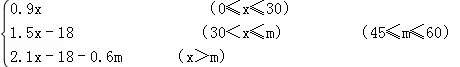为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
考点:
一次函数的应用. | | 分析: | (1)根据房款=房屋单价×购房面积就可以表示出应缴房款; (2)由分段函数当0≤x≤30,当30<x≤m时,当x>m时,分别求出Yy与x之间的表达式即可; (3)当50≤m≤60和当45≤m<50时,分别讨论建立不等式组就可以求出结论. |
| 解答: | 解:(1)由题意,得 三口之家应缴购房款为:0.3×90+0.5×30=42(万元); (2)由题意,得 ①当0≤x≤30时,y=0.3×3x=0.9x ②当30<x≤m时,y=0.9×30+0.5×3×(x﹣30)=1.5x﹣18 ③当x>m时,y=0.3×30+0.5×3(m﹣30)+0.7×3×(x﹣m)=2.1x﹣18﹣0.6m ∴y=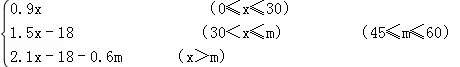 (3)由题意,得 ①当50≤m≤60时,y=1.5×50﹣18=57(舍). ②当45≤m<50时,y=2.1×50 0.6m﹣18=87﹣0.6m. ∵57<y≤60, ∴57<87﹣0.6m≤60, ∴45≤m<50. 综合①②得45≤m<50. |
| 点评: | 本题考查了房款=房屋单价×购房面积在实际生活中的运用,求分段函数的解析式的运用,建立不等式组求解的运用,解答本题时求出函数额解析式是关键. |