еҰӮеӣҫпјҢеңЁзӣҙеӣӣжЈұжҹұABCDпјҚA1B1C1D1дёӯпјҢеә•йқўABCDдёәзӯүи…°жўҜеҪўпјҢABвҲҘCDпјҢABпјқ4пјҢ
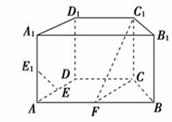 BCпјқCDпјқ2пјҢAA1пјқ2пјҢEпјҢE1еҲҶеҲ«жҳҜжЈұADпјҢAA1зҡ„дёӯзӮ№пјҺ
BCпјқCDпјқ2пјҢAA1пјқ2пјҢEпјҢE1еҲҶеҲ«жҳҜжЈұADпјҢAA1зҡ„дёӯзӮ№пјҺ
пјҲ1пјүи®ҫFжҳҜжЈұABзҡ„дёӯзӮ№пјҢиҜҒжҳҺпјҡзӣҙзәҝEE1вҲҘе№ійқўFCC1пјӣ
пјҲ2пјүиҜҒжҳҺпјҡе№ійқўD1ACвҠҘе№ійқўBB1C1Cпјӣ
пјҲ3пјүжұӮзӮ№DеҲ°е№ійқўD1ACзҡ„и·қзҰ»пјҺ
