直线y＝kx＋m(m≠0)与椭圆W：
＋y2＝1相交于A，C两点，O是坐标原点．
(1)当点B的坐标为(0,1)，且四边形OABC为菱形时，求AC的长；
(2)当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形．
直线y＝kx＋m(m≠0)与椭圆W：＋y2＝1相交于A，C两点，O是坐标原点．
(1)当点B的坐标为(0,1)，且四边形OABC为菱形时，求AC的长；
(2)当点B在W上且不是W的顶点时，证明：四边形OABC不可能为菱形．
(1)因为四边形OABC为菱形，
所以AC与OB相互垂直平分．
所以可设A(t，
)，代入椭圆方程得
＋
＝1，
即t＝±
.
所以|AC|＝2.
(2)假设四边形OABC为菱形．
因为点B不是W的顶点，且AC⊥OB，所以k≠0.
由
消y并整理得
(1＋4k2)x2＋8kmx＋4m2－4＝0.
设A(x1，y1)，C(x2，y2)，则
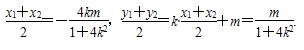所以AC的中点为M
．
因为M为AC和OB的交点，且m≠0，k≠0，
所以直线OB的斜率为－
.
因为k·(－)≠－1，所以AC与OB不垂直．
所以OABC不是菱形，与假设矛盾．
所以当点B不是W的顶点时，四边形OABC不可能是菱形．