已知椭圆![]()
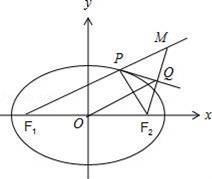
![]() (a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则
(a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则![]()
![]() 的最小值为( )
的最小值为( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.1
D.1
已知椭圆![]()
![]() (a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则
(a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则![]()
![]() 的最小值为( )
的最小值为( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.1
D.1
C【考点】椭圆的简单性质.
【分析】由题意画出图形,利用转化思想方法求得OQ=a,又OQ=2b,得a=2b,进一步得到a,e与b的关系,然后利用基本不等式求得![]()
![]() 的最小值.
的最小值.
【解答】解:如图,由题意,P是以F1,F2为焦点的椭圆上一点,
过焦点F2作∠F1PF2外角平分线的垂线,垂足为Q,
延长F2Q交F1P延长线于M,得PM=PF2,
由椭圆的定义知PF1+PF2=2a,故有PF1+PM=MF1=2a,
连接OQ,知OQ是三角形F1F2M的中位线,
∴OQ=a,又OQ=2b,
∴a=2b,则a2=4b2=4(a2﹣c2),
即c2=![]()
![]() a2,
a2,
∴![]()
![]() =
=![]()
![]() =
=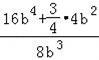

=2b+![]()
![]() ≥2
≥2![]()
![]() =
=![]()
![]() .
.
当且仅当2b=![]()
![]() ,即b=
,即b=![]()
![]() 时,
时,![]()
![]() 有最小值为
有最小值为![]()
![]() .
.
故选:C.