=a,
=b,对于任意点M,点M关于A点的对称点为S,点S关于B点的对称点为N.(1)用a、b表示向量
;
(2)设|a|=1,|b|=2,|
|∈［2
,2
］,求a与b的夹角θ的取值范围.
=a,=b,对于任意点M,点M关于A点的对称点为S,点S关于B点的对称点为N.(1)用a、b表示向量;
(2)设|a|=1,|b|=2,||∈［2,2］,求a与b的夹角θ的取值范围.
思路解析:此题主要考查了向量的表示及运算、中点公式.由(1)中的a、b表示向量及(2)中的条件||∈［2,2］,可利用模来计算a·b的范围,从而求a与b的夹角θ的取值范围.
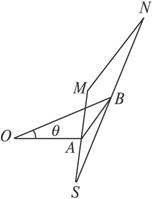
解:(1)依题意,A为MS的中点,B为NS的中点,
∴=2
,
=2
.
∴
=
-
=2(
-
)=2
=2(
-
)=2(b-a).(2)∵|
|∈［2
,2
］,
∴|
|2∈［12,28］.
由(1)得12≤4(b-a)2≤28,
∴3≤b2+a2-2a·b≤7.
∴3≤4+1-2a·b≤7.
∴-1≤a·b≤1.
∵cosθ=
,
∴-
≤cosθ≤
.
∵0≤θ≤π,∴
≤θ≤
.