（本小题满分12分）已知数列
的前n项和为
当数列
是各项为正数且公差为d的等差数列时，求数列
是等差数列的充要条件；
若满足
，是否存在
，使数列为等差数列？若存在求出的值，若不存在，请说明理由。
（本小题满分12分）已知数列的前n项和为
当数列是各项为正数且公差为d的等差数列时，求数列是等差数列的充要条件；
若满足，是否存在，使数列为等差数列？若存在求出的值，若不存在，请说明理由。
解 （1）设数列
的公差为d，则
，由等差数列的性质知，
是等差数列的充要条件是
，即
4分
因此式恒成立，所以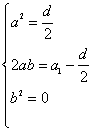
，由此可得
，即为所求的充要条件 6分
（2）等式可化为
，过
是公差为1的等差数列，
，所以
8分
当
时，
，故
，即数列从第3项起每一项与前一项的差是同一个常数，从而为等差数列的充要条件是
10分
即
，
11 分
综上所述，存在使为等差数列 12分