如图，在平面直角坐标系xOy中，点A(0，3)，直线l：y=2x-4，设圆C的半径为1，圆心在直线l上.
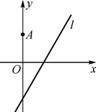
(变式)
(1)若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；
(2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.
如图，在平面直角坐标系xOy中，点A(0，3)，直线l：y=2x-4，设圆C的半径为1，圆心在直线l上.
(变式)
(1)若圆心C也在直线y=x-1上，过点A作圆C的切线，求切线的方程；
(2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.
(1)由
得圆心C为(3，2)，
因为圆C的半径为1，
所以圆C的方程为(x-3)2+(y-2)2=1.
由题知切线的斜率一定存在，设所求圆C的切线方程为y=kx+3，即kx-y+3=0.
所以
=1，所以|3k+1|=
，
所以2k(4k+3)=0，所以k=0或k=-
.
所以所求圆C的切线方程为y=3或y=-x+3，
即y=3或3x+4y-12=0.
(2)因为圆C的圆心在直线l：y=2x-4上，
所以设圆心C为(a，2a-4)，
则圆C的方程为(x-a)2+[y-(2a-4)]2=1.
又因为MA=2MO，所以设点M(x，y)，
则
=2
，整理得
x2+(y+1)2=4，设为圆D.
所以点M应该既在圆C上又在圆D上，
即圆C和圆D有交点.
所以|2-1|≤
≤|2+1|，
由5a2-12a+8≥0得a∈R；
由5a2-12a≤0，得0≤a≤
.
终上所述，实数a的取值范围为[0，].