已知椭圆C：=1（a＞b＞0）过点A，离心率为，点F1，F2分别为其左右焦

已知椭圆C：=1（a＞b＞0）过点A，离心率为，点F₁，F₂分别为其左右焦点．

（1）求椭圆C的标准方程；

（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点P，Q，且？若存在，求出该圆的方程；若不存在，请说明理由．

考点： 圆与圆锥曲线的综合；椭圆的标准方程；直线与圆锥曲线的关系．

专题： 圆锥曲线的定义、性质与方程．

分析： （1）由离心率，推出b=c，利用椭圆经过的点的坐标，代入椭圆方程，求出a、b，即可得到椭圆C方程．

（2）假设满足条件的圆存在，其方程为：x²+y²=r²（0＜r＜1），当直线PQ的斜率存在时，设直线方程为y=kx+b，联立方程组，令P（x₁，y₁），Q（x₂，y₂），利用韦达定理，结合x₁x₂+y₁y₂=0．推出3b²=2k²+2，利用直线PQ与圆相切，求出圆的半径，得到圆的方程，判断当直线PQ的斜率不存在时的圆的方程，即可得到结果．

解答： 解：（1）由题意得：，得b=c，因为，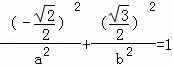

得c=1，所以a²=2，

所以椭圆C方程为．…（4分）

（2）假设满足条件的圆存在，其方程为：x²+y²=r²（0＜r＜1）

当直线PQ的斜率存在时，设直线方程为y=kx+b，

由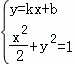得（1+2k²）x²+4bkx+2b²﹣2=0，

令P（x₁，y₁），Q（x₂，y₂），

，…（6分）

∵，∴x₁x₂+y₁y₂=0．

∴，

∴3b²=2k²+2．…（8分）

因为直线PQ与圆相切，∴=

所以存在圆

当直线PQ的斜率不存在时，也适合x²+y²=．

综上所述，存在圆心在原点的圆x²+y²=满足题意．…（12分）

点评： 本题考查椭圆的方程的求法，圆与椭圆的以及直线的综合应用，考查分类讨论思想、转化思想的应用，考查分析问题解决问题的能力．