（04年福建卷理）（14分）已知f(x)=(x∈R)在区间[-1，1]上是增函数。（

（04年福建卷理）（14分）

已知f(x)=(x∈R)在区间[-1，1]上是增函数。

（Ⅰ）求实数a的值组成的集合A；

（Ⅱ）设关于x的方程f(x)=的两个非零实根为x₁、x₂.试问：是否存在实数m，使得不等式m²+tm+1≥|x₁-x₂|对任意a∈A及t∈[-1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由。

解析：（Ⅰ）f＇(x)== ，

∵f(x)在[-1，1]上是增函数，

∴f＇(x)≥0对x∈[-1，1]恒成立，

即x²-ax-2≤0对x∈[-1，1]恒成立.        ①

设(x)=x²-ax-2，

方法一：

①-1≤a≤1，

∵对x∈[-1，1]，f(x)是连续函数，且只有当a=1时，f＇(-1)=0以及当a=-1时，f＇(1)=0

∴A={a|-1≤a≤1}.

方法二：

① 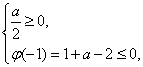   或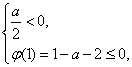

   0≤a≤1     或   -1≤a≤0

   -1≤a≤1.

∵对x∈[-1，1]，f(x)是连续函数，且只有当a=1时，f＇(-1)=0以及当a=-1时，f＇(1)=0

∴A={a|-1≤a≤1}.

（Ⅱ）由=，得x²-ax-2=0，

∵△=a²+8>0

∴x₁，x₂是方程x²-ax-2=0的两非零实根，

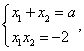∴ 从而|x₁-x₂|==.

∵-1≤a≤1，∴|x₁-x₂|=≤3.

要使不等式m²+tm+1≥|x₁-x₂|对任意a∈A及t∈[-1，1]恒成立，

当且仅当m²+tm+1≥3对任意t∈[-1，1]恒成立，

即m²+tm-2≥0对任意t∈[-1，1]恒成立.        ②

设g(t)=m²+tm-2=mt+(m²-2)，

方法一：

②

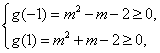
m≥2或m≤-2.

所以，存在实数m，使不等式m²+tm+1≥|x₁-x₂|对任意a∈A及t∈[-1，1]恒成立，其取值范围是{m|m≥2，或m≤-2}.

方法二：

当m=0时，②显然不成立；

当m≠0时，

 ②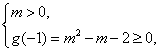或

m≥2或m≤-2.

所以，存在实数m，使不等式m²+tm+1≥|x₁-x₂|对任意a∈A及t∈[-1，1]恒成立，其取值范围是{m|m≥2，或m≤-2}.