解析：这是抽象函数单调性的应用，解题的关键在于处理好f(x·y)=f(x)+f(y)和f(x)+f(x-3)≤2这两个式子，并且要能够将f(x)+f(x-3)≤2转化成与函数的单调性有关.
解：∵f(x)是定义在(0，+∞)上的单调递增函数，
∴x＞3且f(x·y)=f(x)+f(y) ,
∴f(x)+f(x-3)=f(x2-3x),
且x＞3，2=f(2)+f(2)=f(4).
因此f(x)+f(x-3)≤2f(x2-3x)≤f(4),
即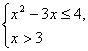
3＜x≤4.
所以x的取值范围是(3,4］.