已知函数
，若方程f（x）=loga（x+2）（0＜a＜1）有且仅有两个不同的实数根，则实数a的取值范围为 ．
已知函数，若方程f（x）=loga（x+2）（0＜a＜1）有且仅有两个不同的实数根，则实数a的取值范围为 ．
[
） ．
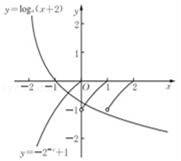
【考点】根的存在性及根的个数判断．
【分析】作出f（x）与y=loga（x+2）的函数图象，根据交点个数判断函数值的大小关系，列出不等式组解出．
【解答】解：∵当x＞0时，f（x）=f（x﹣1），
∴f（x）在（0，+∞）上是周期为1的函数，
做出y=f（x）与y=loga（x+2）的函数图象，则两函数图象有2个交点，
∴
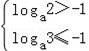，解得
．
故答案为：
．