已知：如图，AB是⊙O的直径，C是⊙O上一点， 过C点的切线与AB的延长

已知：如图，AB是⊙O的直径，C是⊙O上一点， 过C点的切线与AB的延长线交于点D，CE∥AB交⊙O于点E ，连结AC、BC、AE.

（1）求证：①∠DCB=∠CAB；

②；

（2）作CG⊥AB于点G.若（k＞１），求的值（用含k的式子表示）.

（1）证明：①如图10，

解法一：作直径CF，连结BF.

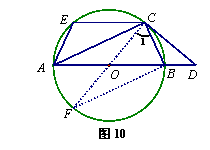∴ ∠CBF=90°，

则 ∠CAB=∠F =90°－∠1.

∵ CD切⊙O于C，

∴ OC⊥CD ，

则 ∠BCD =90°－∠1.

∴ ∠BCD =∠CAB .

解法二：如图11，

连结OC.

∵ AB是直径，

∴ ∠ACB=90°.

则∠2 =90°－∠OCB.

∵ CD切⊙O于C，

∴ OC⊥CD .

则 ∠BCD =90°－∠OCB.

∴ ∠BCD =∠2.

∵ OA=OC，

∴ ∠2 =∠CAB .

∴ ∠BCD =∠CAB .

② ∵ EC∥AB ，∠BCD =∠3，

∴ ∠4 =∠3=∠BCD.

∵ ∠CBD＋∠ABC=180°，

∵ ∠AEC＋∠ABC=180°，

∴ ∠CBD=∠AEC .

∴ △ACE∽△DCB ．

∴ ．

∴ ．

（2）连结EB，交CG于点H，

∵ CG⊥AB于点G， ∠ACB=90°.

∴ ∠3=∠BCG.

∵ ∠3 =∠4.

∴    =

∴ ∠3=∠EBG .

∴ ∠BCG=∠EBG .

∵ （k＞１），

∴ 在Rt△HGB中，.

在Rt△BCG中，.

设HG =a，则BG= ka，CG= k²a. CH=CG－HG=( k²－1)a.

∵ EC∥AB ，

∴ △ECH∽△BGH ．

∴ ．

解法二： 如图10-2，作直径FC，连结FB、EF，则∠CEF=90°.

∵CG⊥AB于点G，

在Rt△ACG中，

设CG =a，则AG= ka，，CF=AB=AG＋BF=（k）a.

∵ EC∥AB ， ∠CEF=90°，

∴直径AB⊥EF.

∴EF=2CG= a.

EC=）=( k)a.

∴.

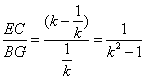解法三：如图11-2，作EP⊥AB于点P，

在Rt△ACG中，

设CG =a，则AG= ka，，

可证△AEP≌△BCG，则有AP=.

EC=AG-AP=（k）a.

∴.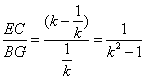