如图,直三棱柱![]() 中,
中, ![]() ,
,![]() .
. ![]() 分别为棱
分别为棱![]() 的中点.(1)求点
的中点.(1)求点![]() 到平面
到平面![]() 的距离;(2)求二面角
的距离;(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
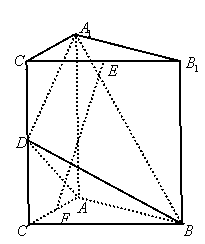 (3)在线段
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
如图,直三棱柱![]() 中,
中, ![]() ,
,![]() .
. ![]() 分别为棱
分别为棱![]() 的中点.(1)求点
的中点.(1)求点![]() 到平面
到平面![]() 的距离;(2)求二面角
的距离;(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
 (3)在线段
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
(必做题)(本小题满分10分)
解:(1)如图所示,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,

![]() 为
为![]() 轴建立空间直角坐标系,由
轴建立空间直角坐标系,由
![]() 可得
可得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
则![]() ,
,![]() ,
,
![]() 设平面
设平面![]() 的法向量为
的法向量为![]() 得
得
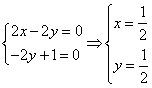 即
即![]() 则取法向量为
则取法向量为![]() ,
,
则点![]() 到平面
到平面![]() 的距离
的距离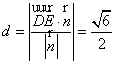 . (3分)
. (3分)
(2)![]() ,
,![]() ,
,![]() 可得
可得![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
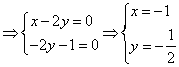 ,
,
故可令![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]()
 ,
,
故可令![]() ,∴
,∴ ,
,
即求二面角![]() 的余弦值为
的余弦值为![]() ; (6分)
; (6分)
(3)假设存在点![]() ,坐标为
,坐标为![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 得
得![]() ,即
,即![]() ,
,
∴![]()
![]()
![]() 即为
即为![]() 中点. (10分)
中点. (10分)