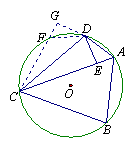
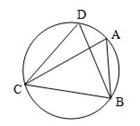
已知A、B、C、D是圆O上的四点，弧CD＝弧BD，AC是四边形ABCD的对角线，（1）如图，连接BD，若∠CDB＝60°，求证：AC是∠DAB的平分线；
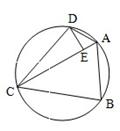
（2）如图，过点D作DE⊥AC，垂足为E，若AC＝7，AB＝5，求线段AE的长度.
已知A、B、C、D是圆O上的四点，弧CD＝弧BD，AC是四边形ABCD的对角线，（1）如图，连接BD，若∠CDB＝60°，求证：AC是∠DAB的平分线；
（2）如图，过点D作DE⊥AC，垂足为E，若AC＝7，AB＝5，求线段AE的长度.
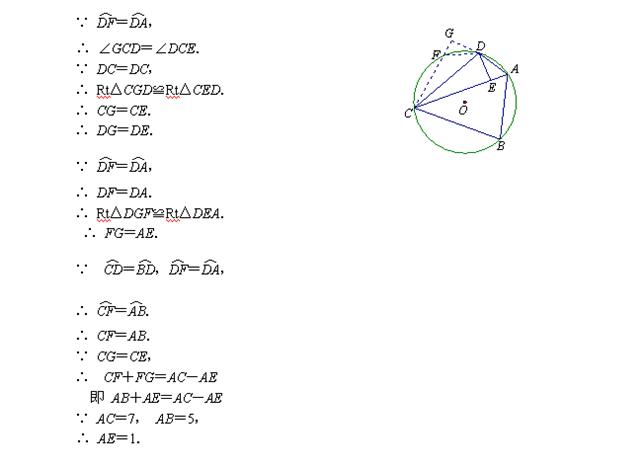
（1）证明：∵ 
＝
，
∴ CD＝BD.
又∵∠CDB＝60°，
∴△CDB是等边三角形.
∴ ∠CDB＝∠DBC.
∴ ＝
.
∴ ∠DAC＝∠CAB.
∴ AC是∠DAB的平分线.
（2）解法一：连结DB.
在线段CE上取点F，使EF＝AE，连结DF.
∵ DE⊥AC，
∴ DF＝DA，∠DFE＝∠DAE.
∵ ＝，
∴ CD＝BD.
∴∠DAC＝∠DCB.
∴ ∠DFE
＝∠DCB.
∵ 四边形ABCD是圆内接四边形，
∴ ∠DAB＋∠DCB＝180°.
又∵∠DFC＋∠DFE＝180°，
∴ ∠DFC＝∠DAB
∵∠DCA＝∠ABD，
∴△CDF≌△BDA.
∴CF＝AB.
∵AC＝7， AB＝5，
∴ AE＝1.
解法二：在上取一点F，使得
＝
，
连结CF，延长CF，过D作DG⊥CF，垂足为G.
