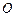 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以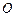 为圆心,
为圆心,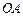 长为半径的⊙
长为半径的⊙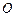 与
与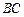 相切于点
相切于点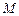 .
.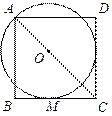
(1)求证:
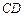 与⊙
与⊙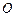 相切;
相切;(2)若⊙
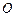 的半径为1,求正方形
的半径为1,求正方形 的边长.
的边长. 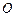 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以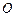 为圆心,
为圆心,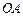 长为半径的⊙
长为半径的⊙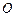 与
与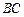 相切于点
相切于点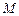 .
.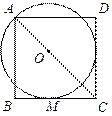
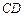 与⊙
与⊙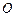 相切;
相切;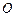 的半径为1,求正方形
的半径为1,求正方形 的边长.
的边长. 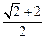 解析:
解析: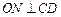 于N,连结OM,则
于N,连结OM,则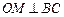 .
.
 的对角线,
的对角线,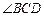 的平分线.
的平分线.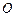 半径,
半径,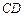 与⊙
与⊙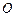 相切. ………….…………………………….3分
相切. ………….…………………………….3分 为等腰直角三角形,OM为半径,
为等腰直角三角形,OM为半径,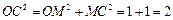 ,
,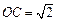

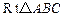 中,AB=BC,
中,AB=BC,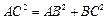
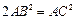
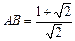 . …….…………………………….5分
. …….…………………………….5分 的边长为
的边长为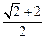 .
.