设{an}是公差d≠0的等差数列，Sn是其前n项的和.
（1）若a1=4，且
，求数列{an}的通项公式；
（2）是否存在
的等差中项？证明你的结论
设{an}是公差d≠0的等差数列，Sn是其前n项的和.
（1）若a1=4，且，求数列{an}的通项公式；
（2）是否存在的等差中项？证明你的结论
解：（1）由
即
将a1=4代入上式并整理得d（12+5d）=0
因为d≠0，解得
所以数列{an}的通项公式为
（2）解：不存在p，q∈N*，且p≠q，使得
的等差中项，证明如下：
因为
所以
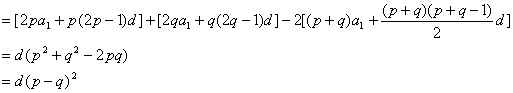
因为d≠0，且p≠q
所以
即不存在p，q∈N*，且p≠q，使得的等差中项