在Rt△ABC中,∠=90°,三角形的角平分线CE和高AD相交于点F,过F作FG
在Rt△ABC中,∠
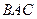
=90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠
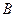
=30°,
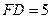
,求四边形
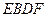
的面积.

略解析:
证明:∵∠BAC=900
AD⊥BC
∴∠1=∠B
∵CE是角平分线
∴∠2=∠3
∵∠5=∠1+∠2
∠4=∠3+∠B
∴∠4=∠5
∴AE=AF……………1分
过F作FM⊥AC并延长MF交BC于N
∴MN//AB
∵FG//BD
∴四边形GBDF为平行四边形
∴GB=FN……………2分
∵AD⊥BC,CE为角平分线
∴FD=FM
在Rt△AMF和RtNDF中
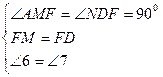
∴△AMF≌△NDF
∴AF=FN
∴AE=BG……………5分
(2)∵∠B=300
AB//NF
∴∠8=300
在Rt△FDN中,FN=2FD=10
∴AF=AE=BG=FN=10
∴∠BAD=600
∴△AEF为等边△
∴EF=AE=10
∵GF//BC
∴∠EGB=∠B=300
∠4=∠9+∠10=600
∴∠9=∠10=300
EG=EF=10
在Rt△ABC中,tan300=
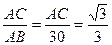
∴AC=10
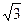
∠2=300
在Rt△CDF中,tan∠
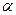
=
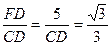
∴CD=
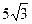
S四EBDF=S△ABC-S△AEC-S△CDF=

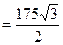
……………10分
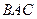 =90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠
=90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠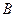 =30°,
=30°,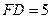 ,求四边形
,求四边形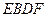 的面积.
的面积.
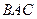 =90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠
=90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠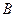 =30°,
=30°,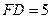 ,求四边形
,求四边形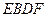 的面积.
的面积.
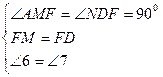
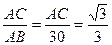
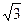 ∠2=300
∠2=300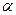 =
=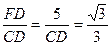
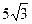

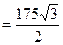 ……………10分
……………10分