（本小题满分12分）
已知函数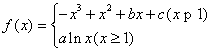
的图象过点（-1，2），且在点（-1，f(-1)）处的切线与直线x-5y+1=0垂直.
（Ⅰ）求实数b，c的值；
（Ⅱ）求f(x)在［-1，e］（e为自然对数的底数）上的最大值.
（本小题满分12分）
已知函数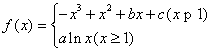的图象过点（-1，2），且在点（-1，f(-1)）处的切线与直线x-5y+1=0垂直.
（Ⅰ）求实数b，c的值；
（Ⅱ）求f(x)在［-1，e］（e为自然对数的底数）上的最大值.
解：（Ⅰ）当x＜时，f ′(x)=-3 x 2+2 x +b，…………………………………………（1分）
由题意得：
，………………………………（3分）
解得：b=c=0. ………………………………………………………………………（4分）
(Ⅱ) 因为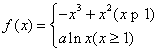
当-1≤x＜1时，f ′(x)=- x (3 x -2),
解f ′(x) ＞0得
∴f (x) 在（-1，0）和（
，1）上单减，在（0，）上单增，
从而f (x)在x=处取得极大值f ()=
又∵f (-1) =2，f (1) =0，
∴f (x) 在［-1，1）上的最大值为2. ……………………………………………………（8分）
当1≤x ≤e时，f (x)=alnx，
当a≤0时，f (x) ≤0；
当a＞0时，f (x) 在［1，e］单调递增；
∴f (x) 在［1，e］上的最大值为a. ……………………………………………………（10分）
∴a≥2时，f (x) 在［-1，e］上的最大值为a；
当a＜2时，f (x) 在［-1，e］上的最大值为2. ………………………………………（12分）