（1）求发射过程中电源提供的电流大小；
（2）若电源输出的能量有4%转换为滑块的动能，则发射过程中电源的输出功率和输出电压各是多大?
（3）若此滑块射出后随即以速度v沿水平方向击中放在水平面上的砂箱，它嵌入砂箱的深度为s′.设砂箱质量为M，滑块质量为m，不计砂箱与水平面之间的摩擦.求滑块对砂箱平均冲击力的表达式.
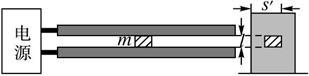
图2-15
（1）求发射过程中电源提供的电流大小；
（2）若电源输出的能量有4%转换为滑块的动能，则发射过程中电源的输出功率和输出电压各是多大?
（3）若此滑块射出后随即以速度v沿水平方向击中放在水平面上的砂箱，它嵌入砂箱的深度为s′.设砂箱质量为M，滑块质量为m，不计砂箱与水平面之间的摩擦.求滑块对砂箱平均冲击力的表达式.
图2-15
解析：(1)由匀加速运动公式
a=
=9×105 m/s2
由安培力公式和牛顿第二定律，有
F=IBl=kI2l,kI2l=ma
因此I=
=8.5×105 A.
(2)滑块获得的动能是电源输出能量的4%，即
PΔt×4%=
mv2
发射过程中电源供电时间
Δt=
=
×10-2 s
所需电源输出功率为
P=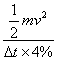
=1.0×109 W
由功率P=IU，解得输出电压
U=
=1.2×103 V.
(3)分别对砂箱和滑块用动能定理，有
=
MV2 
=
mV2-
mv2
由牛顿定律f=-
和相对运动sm=sM+s′
由动量守恒mv=(m+M)V
联立得
=
·
mv2
故平均冲击力
=
·
.
答案：(1)I=8.5×105 A (2)P=1.0×109 W U=1.2×103 V (3)
=
·