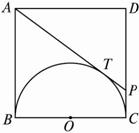
图2-14

图2-14
思路分析
:注意到AB、AT为切线,PT、PC为切线,则想到连结OA、OT、OP,构造切线长定理的基本图形,要求AT∶TP,则只需求AB∶PC,这可以通过解直角三角形或△ABO∽△OCP求得.解法一
:连结AO、TO、OP.∵四边形ABCD为正方形,
∴BC⊥AB,BC⊥CD.
又∵BC为⊙O的直径,
∴AB、DC为⊙O的切线,切点为B、C.
∵AT、AB切⊙O于T、B,
∴AT =AB且∠AOB =∠AOT.
∵PT、PC切⊙O于T、C,
∴PT =PC且∠POT =∠POC.
又∵∠AOB +∠AOT +∠POT +∠POC =180°,
∴∠AOB +∠POC =∠AOP =90°.
又∠ABO =90°,∴∠POC=∠BAO.
∴Rt△ABO∽△Rt△OCP.∴![]() =
=![]() =
=![]() .
.
∴OB =2CP.∴AB =2OC =2OB =4CP,
即AT∶TP =4∶1.
解法二
:先证得∠BAO =∠POC(方法同上).在Rt△ABO中,tan∠BAO =![]() =
=![]() ,
,
在Rt△OCP中,PC =OC·tan∠POC =![]() =
=![]() ×
×![]() =
=![]() ,
,
∴AT∶TP =4∶1.
解法三
:先证得AT =AB,PT =PC(方法同上).设正方形边长为a,PT =PC =x,则PD =a-x.
又∵AT =AB =AD =a,在Rt△ADP中,AD2+DP2 =AP2,
即a2+(a -x)2=(a +x)2,解得![]() .
.
∴AT∶TP =4∶1.