思路解析:本题可以根据圆的性质结合图形进行分析,这里牵涉到角的运算,所以可把圆的方程转化为参数方程进行运算.
解:如右图所示,利用同弧所对圆心角与圆周角的关系,可知∠BOC=120°,B、C两点中,只要一个确定,另一个也确定,为了便于解题,引入圆的参数方程![]()
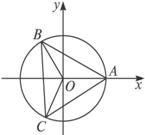
于是,设G(x,y),而点B的坐标记为(rcosθ,rsinθ),则点C的坐标为(rcos(120°+θ),rsin(120°+θ)).
从A、B、C三点互不重合得0°<θ<240°,利用重心坐标公式有
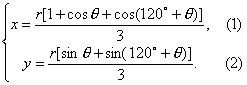
由式①,得3x-r=r[cosθ+cos(120°+θ)],即3x-r=rcos(60°+θ). ③
由式②,得3y=r[sinθ+sin(120°+θ)],即3y=rsin(60°+θ). ④
由③④平方相加可得(x-![]()
由于0°<θ<240°,
所以0≤x=![]()
即△ABC的重心G的轨迹方程是(x-![]()
轨迹是一段圆弧.