（14分）设A．B为椭圆上
的两个动点。
（1）若A．B满足
，其中O为坐标原点，求证：
为定值；
（14分）设A．B为椭圆上的两个动点。
（1）若A．B满足，其中O为坐标原点，求证：为定值；
解析：证明：（1）①若OA，OB的斜率都存在时，设OA方程为
，代入椭圆方程，得
同理，直线OB的方程为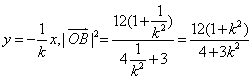
+
②当直线OA．OB的斜率有一条存在另一条不存在时
或
或
（2）
也成立。 …………6分
设
，点
也在椭圆上
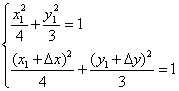两式相减得
，令
得切线的斜率为
，切线方程为
，
再由点A在椭圆上，得过A的切线方程为
……8分
同理过B
的切线方程为：
，设两切线的交点坐标为
，则：
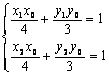，即AB的方程为：
，又
，消去
，得：
。 …………14分