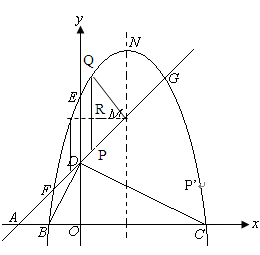
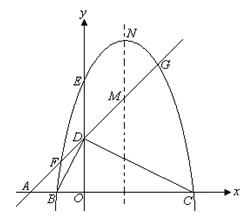
(本小题满分7分)如图,平面直角坐标系中,点A、B、C在x轴上,点D
(本小题满分7分)如图,平面直角坐标系中,点
A、
B、
C在
x轴上,点
D、
E在
y轴上,
OA=
OD=2,
OC=
OE=4,2
OB=OD,直线
AD与经过
B、
E、
C三点的抛物线交于
F、
G两点,与其对称轴交于
M.点
P为线段
FG上一个动点(与
F、
G不重合),
PQ∥
y轴与抛物线交于点
Q.
【小题1】 (1)求经过
B、
E、
C三点的抛物线的解析式;
【小题2】 (2)是否存在点
P,使得以
P、
Q、
M为顶点的三角形与△
AOD相似?若存在,求出满足条件的点
P的坐标;若不存在,请说明理由;
【小题1】(1)B
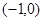
,C

,D
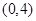
设函数解析式为y=a(x+1)(x-4),则
a×1×(-4)=4,解得a=-1
所以经过
B、
E、
C三点的抛物线的解析式为
y=" -" (x+1)(x-4)=
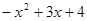
……….3分
【小题2】(2) 直线AD解析式为y=x+2,M(
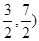
所以M(1,3),过点M作MR⊥PQ于点R,
因为△AOD是等腰直角三角形,结合题意
可知△MPQ是等腰直角三角形
设P(
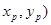
,Q(
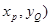
,
PQ∥
y轴与抛物线交于点
Q.
所以
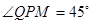
① 当

时 2MR="QP," P

…………………5分
② 当

时 MQ="QP," P
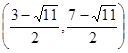
…………………7分解析:
略

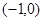 ,C
,C ,D
,D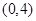
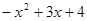 ……….3分
……….3分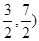

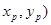 ,Q(
,Q(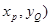 ,PQ∥y轴与抛物线交于点Q.
,PQ∥y轴与抛物线交于点Q.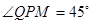
 时 2MR="QP," P
时 2MR="QP," P …………………5分
…………………5分 时 MQ="QP," P
时 MQ="QP," P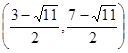 …………………7分解析:
…………………7分解析: