已知奇函数f(x)的定义域为[﹣2,2],且在定义域上单调递减,则满足不等式f(1﹣m)+f(1﹣2m)<0的实数m的取值范围是 .
已知奇函数f(x)的定义域为[﹣2,2],且在定义域上单调递减,则满足不等式f(1﹣m)+f(1﹣2m)<0的实数m的取值范围是 .
[﹣![]()
![]() ,
,![]()
![]() ] .
] .
【考点】奇偶性与单调性的综合.
【专题】计算题;函数思想;转化思想;函数的性质及应用.
【分析】根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
【解答】解:∵函数奇函数f(x)的定义域为[﹣2,2],且在定义域上单调递减,
∴不等式f(1﹣m)+f(1﹣2m)<0等价为f(1﹣m)<﹣f(1﹣2m)=f(2m﹣1),
即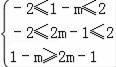
 ,即
,即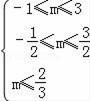
 ,得﹣
,得﹣![]()
![]() ≤m≤
≤m≤![]()
![]() ,
,
故答案为:[﹣![]()
![]() ,
,![]()
![]() ]
]
【点评】本题主要考查不等式的求解,根据函数奇偶性将不等式进行转化是解决本题的关键.注意定义域的限制.