设![]() ,函数
,函数![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)设![]() 问
问![]() 是否存在极值,若存在,请求出极值;若不存在,请说明理由;
是否存在极值,若存在,请求出极值;若不存在,请说明理由;
(3)设![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() 直线
直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
设![]() ,函数
,函数![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)设![]() 问
问![]() 是否存在极值,若存在,请求出极值;若不存在,请说明理由;
是否存在极值,若存在,请求出极值;若不存在,请说明理由;
(3)设![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() 直线
直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
在区间![]() 上,
上,![]() .
.
(Ⅰ) ![]() .
.
(1)当![]() 时,∵
时,∵![]() ,∴
,∴![]() 恒成立,
恒成立,![]() 的单调增区间为
的单调增区间为![]() ;
;
(2)当![]() 时,令
时,令![]() ,即
,即![]() ,得
,得![]()
∴![]() 的单调增区间为
的单调增区间为![]()
综上所述:
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() . ………………… 4分
. ………………… 4分
(Ⅱ) ![]()
得![]()
当![]() 时,恒有
时,恒有![]()
∴![]() 在
在![]() 上为单调增函数,
上为单调增函数,
故![]() 在
在![]() 上无极值; ………………… 6分
上无极值; ………………… 6分
当![]() 时,令
时,令![]() ,得
,得![]()
![]() 单调递增,
单调递增,
![]() 单调递减.
单调递减.
∴![]()
![]() 无极小值
无极小值
综上所述:当![]() 时,
时,![]() 无极值;
无极值;
当![]() 时,
时,![]() 有极大值
有极大值![]() ,无极小值.………………… 8分
,无极小值.………………… 8分
(Ⅲ)证明:![]() ,
,
又![]() ,所以
,所以![]() ,
,
要证![]() ,即证
,即证![]() ,………………… 10分
,………………… 10分
不妨设![]() ,即证
,即证![]() ,即证
,即证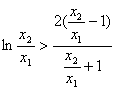 ,
,
设![]() ,即证:
,即证:![]() ,
,
也就是要证:![]() ,其中
,其中![]() ,………………… 12分
,………………… 12分
事实上:设![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递增,因此
上单调递增,因此![]() ,即结论成立.………………… 16分
,即结论成立.………………… 16分