如图①，直线l表示一条东西走向的笔直公路，四边形ABCD是一块边长

如图①，直线l表示一条东西走向的笔直公路，四边形ABCD是一块边长为100米的正方形草地，点A，D在直线l上，小明从点A出发，沿公路l向西走了若干米后到达点E处，然后转身沿射线EB方向走到点F处，接着又改变方向沿射线FC方向走到公路l上的点G处，最后沿公路l回到点A处．设AE=x米（其中x＞0），GA=y米，已知y与x之间的函数关系如图②所示，

（1）求图②中线段MN所在直线的函数表达式；

（2）试问小明从起点A出发直至最后回到点A处，所走过的路径（即△EFG）是否可以是一个等腰三角形？如果可以，求出相应x的值；如果不可以，说明理由．

【分析】（1）根据点M、N的坐标，利用待定系数法即可求出图②中线段MN所在直线的函数表达式；

（2）分FE=FG、FG=EG及EF=EG三种情况考虑：①考虑FE=FG是否成立，连接EC，通过计算可得出ED=GD，结合CD⊥EG，可得出CE=CG，根据等腰三角形的性质可得出∠CGE=∠CEG、∠FEG＞∠CGE，进而可得出FE≠FG；②考虑FG=EG是否成立，由正方形的性质可得出BC∥EG，进而可得出△FBC∽△FEG，根据相似三角形的性质可得出若FG=EG则FC=BC，进而可得出CG、DG的长度，在Rt△CDG中，利用勾股定理即可求出x的值；③考虑EF=EG是否成立，同理可得出若EF=EG则FB=BC，进而可得出BE的长度，在Rt△ABE中，利用勾股定理即可求出x的值．综上即可得出结论．

【解答】解：（1）设线段MN所在直线的函数表达式为y=kx+b，

将M（30，230）、N（100，300）代入y=kx+b，

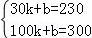，解得：，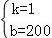

∴线段MN所在直线的函数表达式为y=x+200．

（2）分三种情况考虑：

①考虑FE=FG是否成立，连接EC，如图所示．

∵AE=x，AD=100，GA=x+200，

∴ED=GD=x+100．

又∵CD⊥EG，

∴CE=CG，

∴∠CGE=∠CEG，

∴∠FEG＞∠CGE，

∴FE≠FG；

②考虑FG=EG是否成立．

∵四边形ABCD是正方形，

∴BC∥EG，

∴△FBC∽△FEG．

假设FG=EG成立，则FC=BC成立，

∴FC=BC=100．

∵AE=x，GA=x+200，

∴FG=EG=AE+GA=2x+200，

∴CG=FG﹣FC=2x+200﹣100=2x+100．

在Rt△CDG中，CD=100，GD=x+100，CG=2x+100，

∴100²+（x+100）²=（2x+100）²，

解得：x₁=﹣100（不合题意，舍去），x₂=；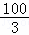

③考虑EF=EG是否成立．

同理，假设EF=EG成立，则FB=BC成立，

∴BE=EF﹣FB=2x+200﹣100=2x+100．

在Rt△ABE中，AE=x，AB=100，BE=2x+100，

∴100²+x²=（2x+100）²，

解得：x₁=0（不合题意，舍去），x₂=﹣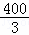（不合题意，舍去）．

综上所述：当x=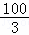时，△EFG是一个等腰三角形．

【点评】本题考查了待定系数法求一次函数解析式、等腰三角形的判定与性质、相似三角形的判定与性质、正方形的性质以及勾股定理，解题的关键是：（1）根据点的坐标，利用待定系数法求出一次函数关系式；（2）分FE=FG、FG=EG及EF=EG三种情况求出x的值．