已知椭圆
以双曲线
的焦点为顶点，以双曲线的顶点为焦点。
（1）求椭圆的方程；
（2）若直线
与椭圆相交于点
,
两点（,不是左右顶点），且以线段
为直径的圆过椭圆左顶点
，求证：直线
过定点，并求出该定点的坐标。
已知椭圆以双曲线的焦点为顶点，以双曲线的顶点为焦点。
（1）求椭圆的方程；
（2）若直线与椭圆相交于点,两点（,不是左右顶点），且以线段为直径的圆过椭圆左顶点，求证：直线过定点，并求出该定点的坐标。
解：（1）
；
（2）设
，联立方程组
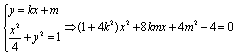，得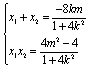
。
又因为以
为直径的圆过点
，所以
,即
，整理得
，所以
或
且满足
，若，则直线
恒过定点，不合题意；若，则直线恒过定点
。