(l3分)已知椭圆
的中心在原点
，焦点在
轴上，直线
与交于
两点，
，且
.
(1)求椭圆的方程；
(2)若
是椭圆上两点，满足
，求
的最小值．
(l3分)已知椭圆的中心在原点，焦点在轴上，直线与交于两点，，且.
(1)求椭圆的方程；
(2)若是椭圆上两点，满足，求的最小值．
解析：（1）设直线
与椭圆
交于
由
,知
而
代入上式得到：
①
而
知：
，即
不妨设
，则
②
由②式代入①式求得：
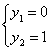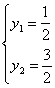
或
或
若不合题意，舍去.
,则椭圆方程为
故所求椭圆方程为……………………………………………………(7分)
（2）
是椭圆上的点，且
故设
于是
从而
又
从而
即
的最小值为
……………………………………………………(13分)