已知两点M(－1，0)，N(1，0)，且点P使
成公差小于零的等差数列.
(1)点P的轨迹是什么曲线？
(2)若点P坐标为(x0,y0),Q为
与
的夹角，求tanθ
已知两点M(－1，0)，N(1，0)，且点P使成公差小于零的等差数列.
(1)点P的轨迹是什么曲线？
(2)若点P坐标为(x0,y0),Q为与的夹角，求tanθ
(1) 点P的轨迹是以原点为圆心，
为半径的右半圆 (2) tanθ=
(1)设P(x,y）,由M(－1，0），N(1，0）得，
=－
=(－1－x,－y）,
=(1－x,－y),
=－
=(2,0),
∴·=2(1+x), ·
=x2+y2－1,
=2(1－x).
于是，
是公差小于零的等差数列，
等价于
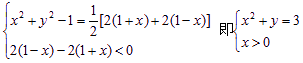
所以，点P的轨迹是以原点为圆心，
为半径的右半圆.
(2)点P的坐标为(x0,y0)
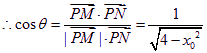
