(本小题共14分)
已知椭圆![]()
![]() 经过点
经过点![]() 其离心率为
其离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,以线段
相交于A、B两点,以线段![]() 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆![]() 上,
上,![]() 为坐标原点. 求
为坐标原点. 求![]() 到直线距离的
到直线距离的![]() 最小值.
最小值.
(本小题共14分)
已知椭圆![]()
![]() 经过点
经过点![]() 其离心率为
其离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,以线段
相交于A、B两点,以线段![]() 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆![]() 上,
上,![]() 为坐标原点. 求
为坐标原点. 求![]() 到直线距离的
到直线距离的![]() 最小值.
最小值.
(共14分)
解:(Ⅰ)由已知,![]() ,所以
,所以![]() , ① …………………1分
, ① …………………1分
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() , ② …………………2分
, ② …………………2分
由①②解之,得![]() .
.
故椭圆![]() 的方程为
的方程为![]() . …………………5分
. …………………5分
(Ⅱ) 当直线![]() 有斜率时,设
有斜率时,设![]() 时,
时,
则由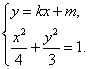
消去![]() 得,
得,![]() , …………………6分
, …………………6分
![]() , ③…………7分
, ③…………7分
设A、B、![]() 点的坐标分别为
点的坐标分别为![]() ,则:
,则:
![]() ,…………8分
,…………8分
由于点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() . ……… 9分
. ……… 9分
从而![]() ,化简得
,化简得![]() ,经检验满足③式.
,经检验满足③式.
………10分
又点![]() 到直线
到直线![]() 的距离为:
的距离为:
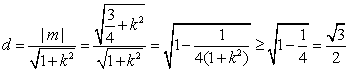 ………11分
………11分
当且仅当![]() 时等号成立 …………12分
时等号成立 …………12分
当直线![]() 无斜率时,由对称性知,点
无斜率时,由对称性知,点![]() 一定在
一定在![]() 轴上,
轴上,
从而![]() 点为
点为![]() ,直线
,直线![]() 为
为![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离为1 ……13分
的距离为1 ……13分
所以点![]() 到直线
到直线![]() 的距离最小值为
的距离最小值为![]() ……14分
……14分