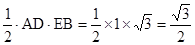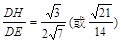两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1.固定△ABC 不动,将△DEF进行如下操作:
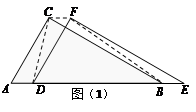
(1)如图(1),△DEF沿线段AB向右平移(即D点在线段AB上移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出 其面积.如果变化,说明理由.
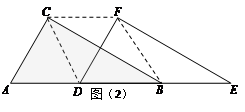
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明 理由.
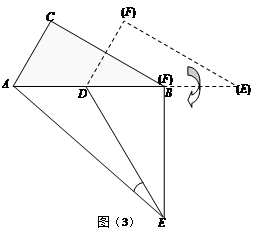
(3)如图(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出 的值.
的值.
(1)不变,理由见解析(2)菱形,理由见解析(3)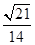
解析:解:(1)解:不变 ………………1分
过C点作CG⊥AB于G,
在Rt△AGC中,∵sin60°=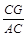 ,∴
,∴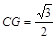
∵AB=2,∴S梯形CDBF=S△ABC= ………4分
………4分
(2)菱形………………5分
∵CD∥BF, FC∥BD,
∴四边形CDBF是平行四边形………………6分
∵DF∥AC,∠ACD=90°,
∴CB⊥DF ∴四边形CDBF是菱形………8分
(3)解法一:过D点作DH⊥AE于H,
则S△ADE=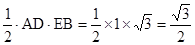
又S△ADE=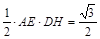 ,
,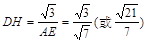
∴在Rt△DHE’中,sinα=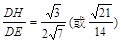 ………………12分
………………12分
解法二:∵△ADH∽△ABE 即: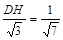
∴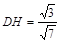 ∴sinα=
∴sinα=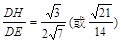
(1)根据三角形全等和同底等高的三角形面积相等,找出面积相等的图形;
(2)根据全等三角形的判定定理解答;
(3)根据三角函数的概念解答



![]() 的值.
的值.
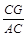 ,∴
,∴