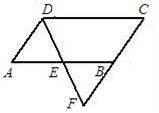
已知▱ABCD中,AB=4,AD=2,E是AB边上的一动点,设AE=x,DE延长线交CB的延长线于F,设CF=y,求y与x之间的函数关系.

已知▱ABCD中,AB=4,AD=2,E是AB边上的一动点,设AE=x,DE延长线交CB的延长线于F,设CF=y,求y与x之间的函数关系.


【考点】相似三角形的判定与性质;根据实际问题列反比例函数关系式;平行四边形的性质.
【分析】由平行四边形的性质,利用“角角”证明△ADE∽△CFD,根据相似三角形对应边的比相等,得出y与x之间的函数关系.
【解答】解:∵四边形ABCD为平行四边形,
∴∠A=∠C,∠ADE=∠F,
∴△ADE∽△CFD
∴![]()
![]() =
=![]()
![]() ,即
,即![]()
![]() =
=![]()
![]() ,
,
∴y=![]()
![]() .
.