(本小题满分13分)
 已知几何体
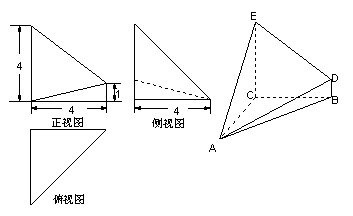
已知几何体![]() 的三视图及直观图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图及直观图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积![]() 的大小;
的大小;
(Ⅱ)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)试探究在![]() 上是否存在点
上是否存在点![]() ,使得
,使得
![]() ,并说明理由.
,并说明理由.
(本小题满分13分)
 已知几何体
已知几何体![]() 的三视图及直观图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图及直观图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积![]() 的大小;
的大小;
(Ⅱ)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)试探究在![]() 上是否存在点
上是否存在点![]() ,使得
,使得
![]() ,并说明理由.
,并说明理由.
解:(Ⅰ)由该几何体的三视图知![]() 面
面![]() ,且EC=BC=AC=4 ,BD=1,
,且EC=BC=AC=4 ,BD=1,
∴![]() .
.
 ∴
∴![]() .
.
即该几何体的体积V为16.
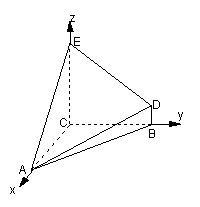
(Ⅱ)以C为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.则A(4,0,0),B(0,4,0),D(0,4,1),E(0,0,4).
∴![]() ,
,
∴![]() ,∴异面直线DE与AB所成的角的余弦值为
,∴异面直线DE与AB所成的角的余弦值为![]() .
.
(Ⅲ)设满足题设的点Q存在,其坐标为(0,m,n),则![]() ,
,
![]() ,
,![]() .
.
∵AQ![]() BQ, ∴
BQ, ∴![]() . ①
. ①
∵点Q在ED上,∴存在![]()
![]() 使得
使得![]() ,
,
∴![]()
![]() .②
.②
②代入①得![]() ,解得
,解得![]() .
.
∴满足题设的点Q存在,其坐标为![]() .
.