(本小题满分12分)
如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 与
与![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() 。
。
(Ⅰ)证明:![]() 四点共面;
四点共面;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 的大小。
的大小。
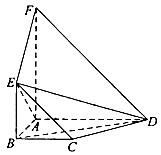
(本小题满分12分)
如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 与
与![]() 都是直角梯形,
都是直角梯形,
![]()
![]()
![]() ,
,![]()
![]()
![]() 。
。
(Ⅰ)证明:![]() 四点共面;
四点共面;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 的大小。
的大小。

(Ⅰ)证明见解析。
(Ⅱ)![]()
解法一:(Ⅰ)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,由
,由![]()
![]()
![]() 得
得
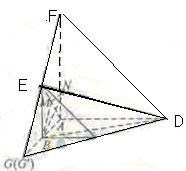
![]()
延长![]() 交
交![]() 的延长线于
的延长线于![]()
同理可得
![]()
故![]() ,即
,即![]() 与
与![]() 重合
重合
因此直线![]() 相交于点
相交于点![]() ,即
,即![]() 四点共面。
四点共面。
(Ⅱ)设![]() ,则
,则![]() ,
,![]()
取![]() 中点
中点![]() ,则
,则![]() ,又由已知得,
,又由已知得,![]() 平面
平面![]()
故![]() ,
,![]() 与平面
与平面![]() 内两相交直线
内两相交直线![]() 都垂直。
都垂直。
所以![]() 平面
平面![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连结
,连结![]()
由三垂线定理知![]() 为二面角
为二面角![]() 的平面角。
的平面角。
![]()
故![]()
所以二面角![]() 的大小
的大小![]()
解法二:由平面![]() 平面
平面![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,以
,以![]() 为坐标原点,射线
为坐标原点,射线![]() 为
为![]() 轴正半轴,建立如图所示的直角坐标系
轴正半轴,建立如图所示的直角坐标系![]() 。
。
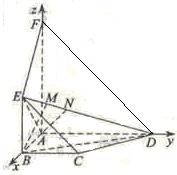
(Ⅰ)设![]() ,则
,则
![]() ,
,
![]() ,
,
故![]() ,从而由点
,从而由点![]() ,得
,得![]() ,
,
故![]() 四点共面。
四点共面。
(Ⅱ)设![]() ,则
,则![]() ,
,
![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,则
,则![]() ,
,
从而![]() ,
,
又![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,则
,则![]() ,
,
从而![]() 。
。
故![]() 与
与![]() 的夹角等于二面角
的夹角等于二面角![]() 的平面角,
的平面角,
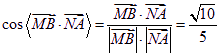 ,
,
所以二面角![]() 的大小
的大小![]() 。
。