如图,在平面直角坐标系![]() 中,点
中,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,将△
,将△![]() 沿
沿![]() 翻折后,点
翻折后,点![]() 落在点
落在点![]() 处.
处.
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)若抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() .
.
①当四边形![]() 为等腰梯形时,求出点
为等腰梯形时,求出点![]() 的坐标;
的坐标;
②当四边形![]() 为平行四边形时,直接写出点
为平行四边形时,直接写出点![]() 的坐标.
的坐标.
如图,在平面直角坐标系![]() 中,点
中,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,将△
,将△![]() 沿
沿![]() 翻折后,点
翻折后,点![]() 落在点
落在点![]() 处.
处.
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(3)若抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的平行线,交抛物线于点
轴的平行线,交抛物线于点![]() .
.
①当四边形![]() 为等腰梯形时,求出点
为等腰梯形时,求出点![]() 的坐标;
的坐标;
②当四边形![]() 为平行四边形时,直接写出点
为平行四边形时,直接写出点![]() 的坐标.
的坐标.
解:(1)如图所示,∵点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
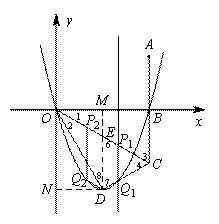 ∴
∴![]() ⊥
⊥![]() 轴于
轴于![]() ,
,![]() ,
,
![]() .…………………………1分
.…………………………1分
∴![]() .
.
∴![]() ,
,
由题意可知 ![]() ,
, ![]() .
.
∴![]() .
.
过点![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
在![]() 中,
中,![]() ,
, ![]() .
.
由矩形![]() 得
得![]() .
.
∵点![]() 在第四象限∴
在第四象限∴![]() .……………………………2分
.……………………………2分
(2)设经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式为
三点的抛物线的解析式为![]() .
.
依题意得 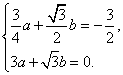 ………………………3分
………………………3分
解得 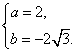 ∴此抛物线的解析式为
∴此抛物线的解析式为![]() .………………………4分
.………………………4分
(3)∵![]() ,
,
∴点![]() 为抛物线的顶点.
为抛物线的顶点.
∴直线![]() 为抛物线的对称轴,交
为抛物线的对称轴,交![]() 于
于![]() ,
,
由题意可知 ![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,![]() .
.
∴![]() .
.
①当点![]() 在
在![]() 上时,四边形
上时,四边形![]() 为等腰梯形.
为等腰梯形.
∵![]() ∥
∥![]() ∥
∥![]() ,
,![]() 与
与![]() 不平行,∴四边形
不平行,∴四边形![]() 为梯形.
为梯形.
要使梯形![]() 为等腰梯形,只需满足
为等腰梯形,只需满足![]() .
.
∵![]() ,∴点
,∴点![]() 在
在![]() 上.
上.
由![]() 、
、![]() 求得直线
求得直线![]() 的解析式为
的解析式为![]() .
.
又∵点![]() 在抛物线上,∴
在抛物线上,∴![]() .
.
解得![]() (与点
(与点![]() 重合,舍).∴
重合,舍).∴![]() 点横坐标为
点横坐标为![]() .
.
由![]() 、
、![]() 求得直线
求得直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在
在![]() 上,∴
上,∴![]() .∴
.∴![]() .………6分
.………6分
②当点![]() 在
在![]() 上时,四边形
上时,四边形![]() 为平行四边形,此时
为平行四边形,此时![]() 点坐标为
点坐标为![]() . ……………………8分
. ……………………8分
综上所述,当![]() 时,
时,![]() 为等腰梯形;当
为等腰梯形;当![]() 时,
时,![]() 为平行四边形
为平行四边形