设
=
，
=（4sinx，cosx﹣sinx），f（x）=•．
（1）求函数f（x）的解析式；
（2）已知常数ω＞0，若y=f（ωx）在区间
是增函数，求ω的取值范围；
（3）设集合A=
，B={x||f（x）﹣m|＜2}，若A⊆B，求实数m的取值范围．
设=，=（4sinx，cosx﹣sinx），f（x）=•．
（1）求函数f（x）的解析式；
（2）已知常数ω＞0，若y=f（ωx）在区间是增函数，求ω的取值范围；
（3）设集合A=，B={x||f（x）﹣m|＜2}，若A⊆B，求实数m的取值范围．
【考点】正弦函数的单调性；集合的包含关系判断及应用；平面向量数量积的运算．
【专题】综合题；转化思想．
【分析】（1）通过数量积的计算，利用二倍角公式化简函数的表达式，化为一个角的一个三角函数的形式，即可．
（2）结合正弦函数的单调增区间，y=f（ωx）在区间
是增函数，说明
⊆
．求出ω的取值范围；
（3）简化集合B，利用A⊆B，得到恒成立的关系式，求出实数m的取值范围．
【解答】解：（1）f（x）=sin2
•4sinx+（cosx+sinx）•（cosx﹣sinx）
=4sinx•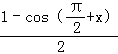
+cos2x
=2sinx（1+sinx）+1﹣2sin2x=2sinx+1，
∴f（x）=2sinx+1．
（2）∵f（ωx）=2sinωx+1，ω＞0．
由2kπ﹣
≤ωx≤2kπ+，
得f（ωx）的增区间是
，k∈Z．
∵f（ωx）在上是增函数，
∴⊆．
∴﹣≥﹣
且
≤，
∴
．
（3）由|f（x）﹣m|＜2，得﹣2＜f（x）﹣m＜2，即f（x）﹣2＜m＜f（x）+2．
∵A⊆B，∴当
≤x≤
时，
不等式f（x）﹣2＜m＜f（x）+2恒成立，
∴f（x）max﹣2＜m＜f（x）min+2，
∵f（x）max=f（）=3，f（x）min=f（）=2，
∴m∈（1，4）．
【点评】本题是中档题，以向量的数量积为平台，考查三角函数的基本公式的应用，函数的单调性，以及函数的值域的求值范围，恒成立的应用，考查计算能力，转化思想．