设m是实数，函数
．
（Ⅰ）求f（x）的定义域；
（Ⅱ）用定义证明：对于任意实数m，函数f（x）在（0，+∞）上为增函数．
设m是实数，函数．
（Ⅰ）求f（x）的定义域；
（Ⅱ）用定义证明：对于任意实数m，函数f（x）在（0，+∞）上为增函数．
【考点】函数单调性的判断与证明；函数的定义域及其求法．
【专题】证明题；函数思想；综合法；函数的性质及应用．
【分析】（Ⅰ）可以看出要使f（x）有意义则需x≠0，这样便得出f（x）的定义域；
（Ⅱ）根据增函数的定义，设任意的x1＞x2＞0，然后作差，通分，便可得到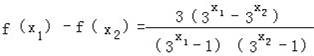
，根据指数函数的单调性便可证明f（x1）＞f（x2），从而得出对任意实数m，函数f（x）在（0，+∞）上为增函数．
【解答】解：（I）解：由3x﹣1≠0得，x≠0；
∴f（x）的定义域是（﹣∞，0）∪（0，+∞）；
（II）证明：设x1＞x2＞0则：
=
；
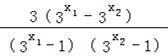
∵指数函数y=3x在R上是增函数，且x1＞x2＞0；
∴
；
∴
；
∴f（x1）＞f（x2）；
∴对于任意实数m，函数f（x）在（0，+∞）上为增函数．
【点评】考查函数定义域的概念及求法，增函数的定义，以及根据增函数的定义证明一个函数为增函数的方法和过程，作差的方法比较f（x1），f（x2），作差后，是分式的一般要通分，以及指数函数的单调性．