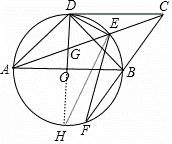
如图，在⊙O中，半径OD⊥直径AB，CD与⊙O相切于点D，连接AC交⊙O于点E，交OD于点G，连接CB并延长交⊙于点F，连接AD，EF．
（1）求证：∠ACD＝∠F；
（2）若tan∠F＝
①求证：四边形ABCD是平行四边形；
②连接DE，当⊙O的半径为3时，求DE的长．
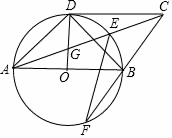
如图，在⊙O中，半径OD⊥直径AB，CD与⊙O相切于点D，连接AC交⊙O于点E，交OD于点G，连接CB并延长交⊙于点F，连接AD，EF．
（1）求证：∠ACD＝∠F；
（2）若tan∠F＝
①求证：四边形ABCD是平行四边形；
②连接DE，当⊙O的半径为3时，求DE的长．
【解析】（1）证明：∵CD与⊙O相切于点D，∴OD⊥CD，
∵半径OD⊥直径AB，∴AB∥CD，∴∠ACD＝∠CAB，
∵∠EAB＝∠F，∴∠ACD＝∠F；
（2）①证明：∵∠ACD＝∠CAB＝∠F，∴tan∠GCD＝tan∠GAO＝tan∠F＝
，
设⊙O的半径为r，在Rt△AOG中，tan∠GAO＝
＝，∴OG＝r，∴DG＝r﹣
r＝
r，
在Rt△DGC中，tan∠DCG＝
＝
，∴CD＝3DG＝2r，∴DC＝AB，
而DC∥AB，∴四边形ABCD是平行四边形；
②作直径DH，连接HE，如图，OG＝1，AG＝
＝
，CD＝6，DG＝2，CG＝
＝2，∵DH为直径，∴∠HED＝90°，∴∠H+∠HDE＝90°，
∵DH⊥DC，∴∠CDE+∠HDE＝90°，∴∠H＝∠CDE，
∵∠H＝∠DAE，∴∠CDE＝∠DAC，
而∠DCE＝∠ACD，∴△CDE∽△CAD，
∴
＝
，即
＝
，∴DE＝
．
