如图，是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=1，它与x轴的一个交点为A（3，0），根据图象，可知关于x的一元二次方程ax2+bx+c=0的解是 ．
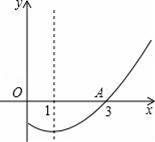
如图，是抛物线y=ax2+bx+c的一部分，其对称轴为直线x=1，它与x轴的一个交点为A（3，0），根据图象，可知关于x的一元二次方程ax2+bx+c=0的解是 ．
3或﹣1 ．
【考点】抛物线与x轴的交点．
【分析】根据抛物线与x轴的两个交点到对称轴的距离相等，设另一个交点为（x，0），可得
=1，解得x的值，关于x的一元二次方程ax2+bx+c=0的解就是抛物线与x轴交点的横坐标．
【解答】解：设抛物线与x轴的另一个交点坐标为：（x，0），
∵抛物线与x轴的两个交点到对称轴的距离相等，
∴=1，
解得：x=﹣1，
∴抛物线与x轴的另一个交点坐标为：（﹣1，0），
∴关于x的一元二次方程ax2+bx+c=0的解是3或﹣1．